First Evidence of Affine Symmetry in Hand Movement
Measurements reveal powerful symmetries in the way humans move their hands, a result that may have important implications for robotics
"A fundamental problem in neuroscience is to understand how human movements are planned and executed." So begins an interesting paper today by Quang-Cuong Pham at the Collège de France and Daniel Bennequin at the Institut de Mathématiques de Jussieu, both in Paris.
Evolution has had many millions of years to refine the process of movement so it's easy to imagine that nature must have discovered many useful shortcuts that help in planning and executing.
Indeed, researchers have found evidence that the human motor system seems to exploit various kinds of symmetries in the way it executes movement.
For example, when humans draw the same shape in different sizes, they do it in the same duration. In other words, they take the same time to draw a short line as a long one. This is known as the isochrony principle.
According to Quang-Cuong and Bennequin, this is good evidence that there is some kind of central control over movement planning. So in an effort to better understand this mechanism, they have devised an interesting experiment to directly measure some of its qualities. And today they publish the results.
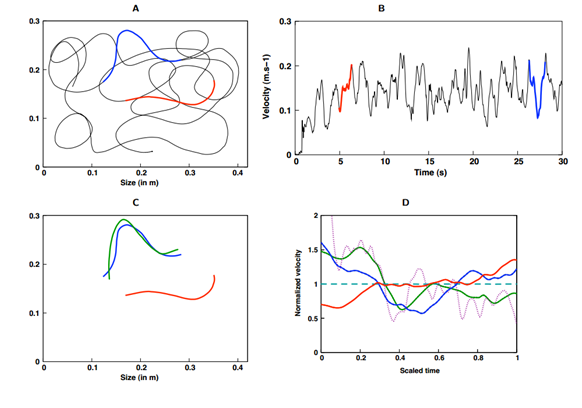
These guys recorded the hand movements of four people as they scribbled onto a sheet of paper slowly and then as they did it again quickly. This experiment recorded not only the shape of the hand movements but the speed as well.
Quang-Cuong and Bennequin compared the fast and slow scribbles, looking for line segments with similar shapes. They then used a computer to find mathematical functions called affine transformations that changed one line shape into the other.
Affine transformations are special because although they distort shapes, they preserve features such as parallel lines and the ratio of distances along these lines.
Having found the appropriate affine transformation for a pair of line segments, Quang-Cuong and Bennequin then applied the same transformation to the time it took to draw the line, with surprising results.
Their main finding is that the same function that transforms the shape of one line segment into another also transforms the temporal structure of the line into the other.
That's a fascinating result. It shows there is some kind of invariance at work in the control and planning of hand movements in humans.
What it doesn't show, however, is how and why this symmetry arises. Is it the result of the way the brain processes movement data (ie a software trick) or linked to the mechanics of body movement (ie a hardware trick)?
Or perhaps there is some other reason. One intriguing possibility is a link to the Webber-Fechner law, which we've discussed on this blog before. This law describes the relationship between the physical magnitude of a stimulus and its perceived intensity, which follows a power law.
What's interesting here is that the law has a formal mathematical correspondence with the theory of communication which describes the way information is transmitted.
That may be coincidence or it may be a clue to a deeper link between perception and interaction and the nature of information
Could it be that the affine symmetry in hand movement is a consequence of the laws that govern the way information is transmitted and received?
Perhaps. Clearly, there is more work to be done here and the scene is set for an explosion of result sin this area since there are all kinds of new ways to record and study body movement.
This kind of work ought to be of huge interest to the robotics community. If powerful symmetries lie behind the way humans move, then there may be huge gains to be had by copying the same trick for robotic movement.
Found here